Degrés et pourcentages
Le pourcentage n'implique aucune unité particulière, c'est d'ailleurs pour ça qu'un pourcentage est une valeur sans unité (c'est en fait…
En cette saison, rien de tel qu’une petite journée à la neige, à dévaler des pistes poudreuses et pentues. De la poudreuse jusqu’aux genoux c’est facile à mesurer, mais qu’en est-il de la pente ?
Si la plupart des gens comprennent bien les pentes en degrés, le pourcentage semble une notion plus vague (pour preuve, le nombre de forums ou les avis divergent sur le sujet).
La pente est définie par Le Trésor de la Langue Française informatisé comme la « tangente trigonométrique (exprimée par une fraction ou en pourcentage) de l’angle formé avec le plan horizontal », c’est à dire la différence d’altitude divisée par la distance HORIZONTALE entre deux points. J’insiste sur l’horizontale ; vous comprendrez pourquoi plus bas.
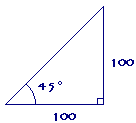
Pour une pente de 45°, nous avons donc un triangle isocèle (et rectangle puisqu’on travaille sur la verticale et l’horizontale de la pente). Si la différence d’altitude est de 100, la distance horizontale est de 100, ce qui nous donne une pente de « 100 pour 100 ».
La mesure de la pente est aisée sur carte topographique. Il suffit de calculer la différence d’altitude entre 2 points, puis de mesurer la distance entre les deux points, et calculer ainsi le pourcentage (en prenant en compte l’échelle de la carte pour la distance entre les 2 points).
Sur le terrain par contre, on a tendance à faire une approximation en prenant la différence d’altitude et en la divisant par la distance parcourue (l’hypoténuse de notre triangle rectangle). Pour des pentes très faibles le calcul revient presque au même (puisque l’hypoténuse est presque aussi longue que le côté horizontal), mais plus la pente est raide et plus l’approximation est fausse.
Une pente proche de 90° n’est donc pas une pente à 100% comme on peut parfois le lire, mais une pente dont le pourcentage tend vers l’infini.
Bienvenue en tant que contributeur 🙂
En voyant le titre de l’article, je pensais que ça concernerait les degrés et pourcentages d’alcool dans les boissons 🙂
Après un coup d’oeil rapide à Wikipedia, il semble que degré et % indiquent la même chose pour l’alcool, contrairement aux pentes.
Article intéressant en tout cas.
Ah ! Monsieur Eusebio a maintenant son propre compte ! Welcome ! 🙂
Ouaip, bienvenue au club ^^
C’est marrant, je pensais justement à la chute de l’article (sans jeu de mot) pendant la lecture, à savoir le pourcentage d’une pente à 90°. Du coup, j’ai plus grand chose à dire dans ce commentaire :-/
Intéressant au passage, j’ai toujours pensé que le pourcentage était par rapport à l’hypoténuse !
Ouf, mon examen d’entrée semble s’être bien passé 🙂
Content d’avoir été exhaustif.
Cela me rappelle un prof de physique qui soutenait mordicus le rapport à l’hypoténuse.Il le soutenait d’autant plus qu’un de ses problèmes posés en examen y faisait référence. Preuves écrites à l’appui, cela a fini par un « De toute façon, les encyclopédistes sont des lettrés qui ne comprennent rien à la physique. » 🙂
Bonjour
une autre façon de décrire les pentes :
cette méthode est utilisée sur les chantiers pour s’adresser aux chauffeurs d’engins qui taillent les talus.
on parle en tant pour tant, comme les pourcentages mais on utilise l’unité, c’est comme çà que 100 % devient 1 pour 1,
le cas le plus courant est 3 pour 2, pour la stabilité des matériaux, on avance de trois, on descend de deux, soit 66.6666 %
je ne sais pas mettre de pièce jointe pour expliciter mes dires.
amicalement
Le pourcentage n’implique aucune unité particulière, c’est d’ailleurs pour ça qu’un pourcentage est une valeur sans unité (c’est en fait le quotient de deux grandeurs). Donc le calcul de pente des ouvriers est exactement le même que celui des mathématiciens.