Calcul de la circonférence d’une latitude
le prof nous a demandé de calculer la distance en km entre l'equateur du cancer 23°36'33"N et cercle arctique 66°30'N…
Ce billet est en deux parties et permettra de connaitre la vitesse de rotation d’un point sur la Terre.
La méthode de calcul d’une circonférence d’une latitude est assez complexe. Les calculs se baseront sur le rayon de la Terre : 6378 km.
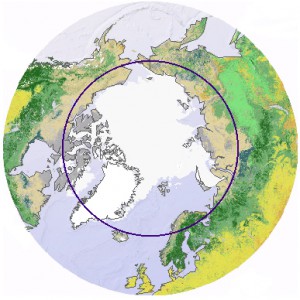
Une latitude est définie en degré (environ 45° N pour le 45° parallèle, environ 66° N pour le Cercle Polaire Arctique).
Pour calculer la circonférence d’un cercle, il nous faut connaitre son rayon et le multiplier par 2 pi. Le calcul du Cosinus de cet angle nous donnera le rapport entre le rayon de la Terre à l’équateur et le rayon de la lattitude en question.
La formule pour calculer la circonférence d’une latitude est donc :
2 * pi * (cos(L) * R) .
- L est le degré de Latitude
- R est le rayon de la Terre
- Valeur de pi
La circonférence de l’équateur est donc :
- 2 * pi * cos(0) * 6378 = 40074 km
La circonférence du 45° parallèle Nord est donc de
- 2 * pi * cos(45) * 6378 = 28336 km
La circonférence du cercle polaire Arctique est donc de :
- 2 * pi * cos(66) * 6378 = 16300 km
Comment trouve-t-on le cosinus de la latitude de 38o 54′?
Merci
38°54′ correspond à 38.9°. Ensuite, que ce soit 38,9°N ou 38,9°S, le cosinus reste le même et cos(38,9°)=0,77824315.
je veux connaitre comment calculer la 60 eme parallèle de la planète
C’est écrit assez clairement :
circonférence = 2 * Pi * R * cos(L)
Dans ton cas, L = 60° = Pi / 3 rad (ça fait à peu 1,05)
pardan mais j’ai pas compris pour quoi? pi/ 3 rad
C’est une question de conversion d’angles.
Un angle de 180° correspond à un angle de Pi radians. C’est une conversion linéaire, donc 60°=Pi/3 rad.
De manière générale, les fonctions trigonométriques prennent des arguments en radians, d’où la nécessité de la conversion.
Bonjour Bastien,
Peut on dire, qu’une mesure faite sur notre planète (calcul d’une longueur entre deux latitudes ou longitudes) est bien une mesure de longueur et non (et ou) une mesure d’angle ?
Car, dans l’absolu puisque notre planète est ronde finalement tout est affaire d’angle …
Moi je cherche une mesure de longueur (dans une chasse au trésor) et si je trouve :
un point sur une latitude à laquelle j’ajoute tant de degrés, minutes, secondes pour arriver sur un autre point, est ce que la longueur entre ces deux points est considérée comme une mesure de longueur ou pas ?
Woué je m’explique peut être mal … En tout cas merci pour votre page. Amitiés.
En excel, les fonctions trigonométriques sont exprimées en radians, pas en degrés.
il faut d’abord convertir en utilisant la fonction radians(45)
bonjour ,comment mesurent une distance entre deux latitudes et les niveaux des memmes
Bonjour, je n’arrive pas a transposer 2 * pi * cos(LAT) * 6378 = 28336 km dans Excel… cela me donne 21’051.8353 pour une lat de 45° ???
merci d’avance,
Didier
Ce n’est pas exact vers le pôle, car il faut tenir compte de l’aplatissement de la Terre, R n’est plus égal à 6378 km comme à l’équateur, mais à 6356 km.
découverte intéressante, merci tout simplement
magnifique
Merci pour ce partage de connaissances utiles 🙂
le prof nous a demandé de calculer la distance en km entre l’equateur du cancer 23°36’33″N et cercle arctique 66°30’N
avec un mile nautique= 1.8km